Las matemáticas representan el mas alto nivel de abstracción que puede alcanzar la mente humana, pero es una creencia muy habitual el que fueron los egipcios y los babilonios los pueblos con mayores  habilidades matemáticas. Sin embargo no debemos de olvidarnos de la India.

Hacia el tercer milenio a.C. se desarrolló allí una civilización que tuvo un gran nivel  matemático. Era la llamada   «civilización del Indo«, (también llamada civilización Harappan) identificada en el año 1921 en el valle del Indo y en la ciudad de igual nombre en el Punjab que un año más tarde, se confirmó por el descubrimiento de la de Mohenjo-Daro, cerca del Río Indus en Sindh (sitios que ahora se encuentran en Pakistán). 

La civilización del Indo empezó a desarrollarse hacia el año 2500 a.C. y perduró hasta el 1700 a.C. demostrando tener grandes conocimientos de las matemáticas. Parece ser que aquellos conocimientos matemáticos  y geometricos los habían heredado de épocas muy remotas. Los textos más antiguos de aquellas primitivas matemáticas hindúes son los llamados los «Shulba Sutras»  de Baudhayana,  Apastamba y Katyayana y forman parte de la literatura del período denominado edad Védica. En los mismos se habla de la medición y construcción de altares para los ritos religiosos, y nos muestran una compilación de los procesos matemáticos utilizados para el diseño y construcción de aquellos altares. 

En la religión védica cada hogar debía de tener tres tipos de fuegos de sacrificio (agnis) y el altar apropiado para ellos eran las figuras cuadradas, circulares o semicirculares. Sin embargo, los altares más elaborados,correspondían  a rituales complejos que debían  ser llevados a cabo por los brahmanes y están  referenciados en los Vedas samhitas como el Rigveda.  Probablemente los «Shulba Sutras»  son versiones actualizadas de unos conocimientos que ya venían de varios siglos atrás.

Los altares vedicos más complejos tenían usualmente forma de halcón. En sus libros sagrados se afirma que aquél que desee el cielo debe de construir su altar de esta forma, ya que el halcón es el ave mejor voladora, y de este modo el ofrendante-convertido en halcón-podria volar mejor hacia el mundo celestial.

El «altar del halcón» se lo remito a este magnifico artículo  en el que se explican detalladamente las formas de desarrollar la geometría de aquellos altares Védicos que con sus diseños elaborados, requerían mediciones muy precisas para obtener unos resultados espectaculares 

 Para la construcción  de estos altares (vease el artículo citado) usaban «códigos de cuerda» con medidas exactas y diferentes formas geométricas. Muchos de aquellos cálculos empleaban  la fórmula geométrica del teorema de Pitágoras y en los «Shulba Sutras» podemos ver una declaración explícita del citado teorema de Pitágoras 

Y su aplicación práctica como la construcción de un cuadrado de área igual a la suma o diferencia de dos cuadrados. El Teorema de Pitágoras ya era conocido por los matemáticos de la India en el siglo VIII antes de Cristo y aquellas  construcciones implicaban  la aplicación de identidades  algebraicas como

 (a ± b)2 = a2 + b2 ± 2ab

 

Los primeros ejemplos conservados de este sistema de numeración se encontraron  en varias columnas de piedra de un promedio de entre 12 y 15 m de altura, con un peso de hasta 50 toneladas, erigidas en la India por el Rey Ashoka durante su reinado en el siglo III a.C.

.   (Imagen Wikipedia)

También nos aparecen en algunas  inscripciones en cuevas y monedas en las regiones hindúes cercanas a Poona,  Bombay y Uttar Pradesh. Se trata de los llamados «numerales Brahmi» que consistían en un sistema de numeración de base 10 nacido hacia la mitad del siglo tercero a.C. El sistema de numeración decimal de base diez, es la base numérica más ampliamente utilizada por las civilizaciones modernas. 

Este ingenioso método de expresar cada número posible utilizando un conjunto de diez símbolos y en el que cada símbolo tiene un valor de lugar y un valor absoluto  evolucionó posteriormente hacia  los numerales Gupta que corresponden al período en el que la dinastía Gupta  gobernó el estado de Magadha en el noreste de la India, entre los siglo IV y VI d.C. y a los numerales Nagari, (a veces llamados los números Devanagari) que surgieron alrededor del siglo VII d.C. y que continuaron desarrollándose desde el siglo XI en adelante. Su nombre significa literalmente «la escritura de los dioses«. Las tres tablas siguientes representan aquellos números indios y su evolución.

Fuente de la imagen

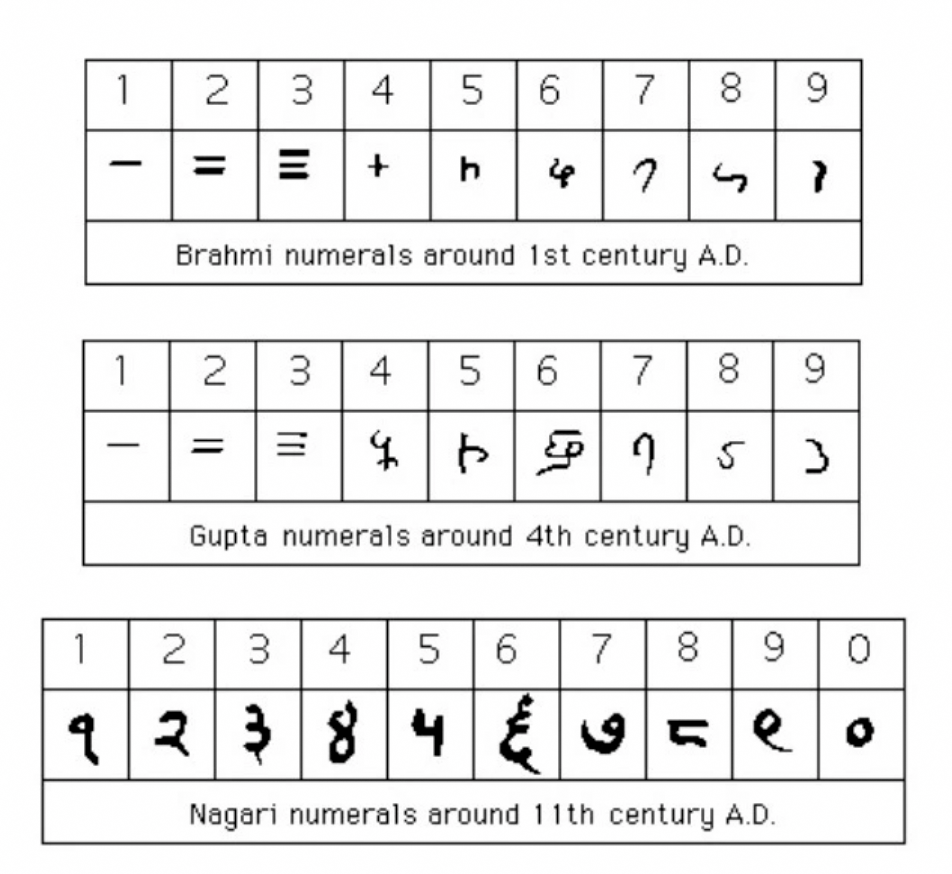
Pero la simplificación vino cuando en la India se Introdujo el concepto del cero  (al que llamaban «sunya«) . El uso único de los símbolos del 1 al 9, conducía a la ambigüedad porque un número como el 54, lo mismo podía  significar esa cantidad que  540, 504 o 5004, por eso el «cero» es el gran aporte de la cultura hindú a las matemáticas, aunque las primeras civilizaciones necesitaron mucho tiempo para adaptarse a este concepto, ya que les costaba asimilar que el cero fuese un número, porque para ellos los números eran «una cantidad de cosas’ y «la nada» no podían entenderla como cantidad. El concepto del cero como un número y no meramente como un símbolo de separación apareció en la India alrededor del 500 d.C y sobre el 650 d.C, su uso ya era habitual en las matemáticas indias. Una tablilla de piedra, encontrada en Gwalior, un templo de Vishnu al sur de Delhi, nos lo mostró por primera vez  en unos números fechados hacia el año 876 d.C .

Dentro de la cámara del citado templo, y a mano derecha de Vishnu, hay una tableta que registra la fecha (en la época local, iniciada seria sobre el 57 a.C.), de la dimensión de una concesión de tierras a un templo vecino y el tamaño de un regalo diario de flores que debía ser pagado por una donación hecha al citado templo. 

Lo sorprendente de estas cifras es que los números de aquella tablilla, fechados hacia el año 876 d.C  son muy parecidos a los números modernos, salvo por el hecho de que los ceros son más pequeños y están un poco mas alzados. 

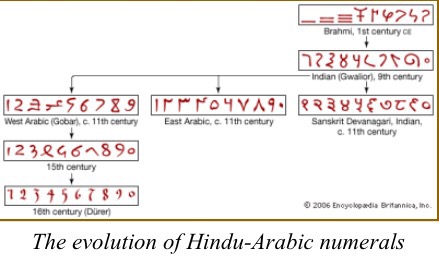
 Los numerales Nagari se extendieron posteriormente hasta Arabia y desde allí al resto del mundo a través del imperio árabe. Los europeos los llamaron «Notaciones árabes,» y los árabes los llamaban «Figuras Indias» (Al-Arqan-Al-hindú). A las matemáticas en sí mismas las llamaban  «el arte indio » (hindisat).  

 Al Biruni un erudito del siglo X hizo  grandes elogios de la «Matemática hindú» y los estudiosos del Medio Oriente que entraron en contacto con la India absorbieron  sus métodos de cálculo con gran entusiasmo que posteriormente fueron transmitidos  a Europa. 

Es probable que las matemáticas emergieran en la India por la necesidad de medir las tierras de labranza o de controlar las transacciones financieras, las ganancias y los impuestos y la rígida jerarquía de castas y de clases sociales hizo que alli , el «misterio de los números» quedara reservado para la élite de los Brahmins y guardado celosamente. De hecho, su transmisión era deliberadamente complicada, tal y como se refleja en el desconcertante canto rítmico del matemático Aryabhatta del sigo V d.C. que dice: «makhi-bhakhi-phakhi- dhaki-nakhi-nakhi-nakhi-hasjha-skaki-kisga-sghaki-kighva-ghaki…». Lo que en realidad se está transmitiendo en este canto son  una lista de valores trigonométricos que cualquier aspirante a matemático debía aprenderse de memoria, de la misma manera que se aprendía los versos del Bhagavad-gita  (texto sagrado hinduista).

Por eso los  indios destacan por sus conocimientos matemáticos y su pensamiento abstracto, y estan habilidades los han llevado a despuntar en las nuevas tecnologías. Cuando vemos que hay una larga lista de dirigentes indios a mando de algunas de las empresas más importantes del mundo como  Indra Nooyi, CEO de Pepsi, Anshu Jain, CoCEO de Deutsche  Bank, o Ivan Menezes, CEO de Diageo, comprobamos que los hindúes ocupan los «puestos claves» de las grandes corporaciones, porque son personas que llevan en sus genes la sabiduría de sus antepasados.

Fuentes:

Kim Plofker. Mathematics in India. Universidad de Princeton